Finding the sweet spot move!

So, I am a noob at chess. The only way to get to some interesting lines is to research what better players are doing and compare it with suggestions from Stockfish, the god of chess. But there is a clear discrepancy between what people play and what SF recommends, as I am sure you are aware.

I was thinking about this today and it struck me that moves are like a product you are trying to buy. The best product is too expensive, the cheapest product is too stupid. You want the sweet spot, that specific item that would do the most for the buck. What if we could apply the same idea to chess?

Consider a gambit. That move has high chances to bring you an advantage with most adversaries, even if some will crush you. It's like a family car move, it does the job on most roads, but on some it will just break down.

Using this analogy, we have to define as best as possible the concepts of price and quality. Quality is easy, we have Stockfish Magazine to tell us how great or bad our car is. It's the price that is hard to define. But in a way, we have that as well. It all depends on the depth at which that move became a candidate. You could use the number of nodes that the engine looked at in order to find the move as decent enough. Not winning, mind you, just not totally losing.

How would that work? First the definitions:
- the optimal evaluation is the evaluation at the highest engine depth for the position
- a candidate move is one that had - at any engine depth - been close enough to it; let's say 100-200 centipawns from optimal
- the quality of a move is the evaluation at the highest depth for a move
- the price of a move is the lowest depth at which the move was considered a candidate

That means that you can show the evaluation of the engine something like this: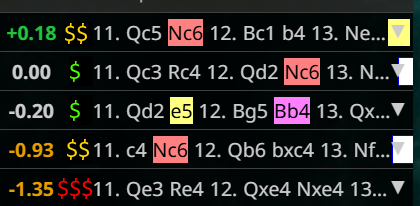
This is just an example, I've added the $ signs arbitrarily, but you would read it like this: Qc5 is the best move, but it's a bit high level. Qc3 and Qd2 are OK and they are also easy to find. c4 is just as hard to find as the best move, but much worse, while Qe3 is bad and hard to find.

Obviously, since the purpose of this particular example is to show the price of the moves as Stockfish calculates the best move, a candidate move becomes just any of those in the list. In other types of systems one might need to get the list of candidate moves and ask the engine to evaluate all of them again, to get a consistent evaluation at the same depth.

Now, I don't know if that would help, but it intuitively feels like something useful. While trying to consider which move to use in your repertoire, the move that costs too much might not be the right one. Conversely, on their turn, if the move that wins is too expensive, maybe you can risk assuming your opponent won't find it.

This concept feels as more grounded in reality than whatever a different engine thinks about the moves and it's a consistent and predictable result.

What do you guys think?