Extended Ease Metric (1)

Intro

Hey all, I'm back after some time to write about something I have been working on since my last blog post. In this blog, I will talk about implementing and extending the math behind the Ease metric formula that was published by @matstc here. Feel free to read the blog to refresh your memories, but in summary, the formula that matstc came up with allowed us to objectively put a number on a position on how easy the position is for humans. The formula mainly used the Leela policy head and a list of candidate moves to come up with a score for a given position. I will quote the exact details from the blog here, so it's easy to read my extension of the ease metric below.

This policy value is the output of a neural network that could be interpreted as reflecting the intuition of a very strong player. For many players, this might be too strong, but I think this is a good start. It’s also beneficial to be exposed to stronger intuition than ours in order to learn from it. As long as the policy value does not rely on millions of calculations, I am happy to use it as a proxy for how natural a move can look to humans.
So for all the possible moves, Leela Chess Zero gives us a policy value P (how natural the move is) and an evaluation Q (how good the move actually is). I am using these values in a weighted sum to describe how close the natural moves are to the best move:

Where:

• Pi is the probability (policy value percentage from 0 to 100) for candidate move i
• Qi is the final evaluation from −1 (certain loss) to +1 (certain win) for candidate move i
• Qmax is the highest Q value across all candidate moves
• α controls the bias to give more resolution at the top end (here set to 1/3)
• β controls the emphasis on high-probability moves (here set to 1.5)

A position close to 1 is easy as pie and a position close to 0 is treacherous. - @matstc

Extended Ease Metric

My extended ease metric is more on the technical/code side than the formula itself. I wanted to integrate the Stockfish engine into Qi and Qmax, as this will provide us with evaluation from the engine and suggest real candidate moves that are considered top moves, let's say N top candidate moves. For Pi will still be from Leela policy head, and α, β will still be the same as in the original formula. Given that Qi and Qmax will be associated with Stockfish, and Stockfish itself doesn't generate such values, we will take Stockfish's centipawn eval cp and convert to Qi by this function below.

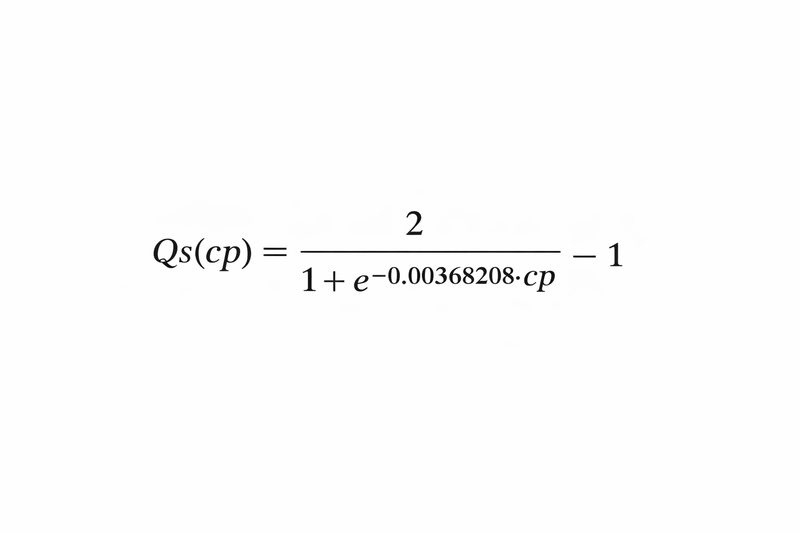
(This function was taken from Lichess PR, which fixes the accuracy of the winning chance function that is used on Lichess for accuracy calculation.)

Applying this convertor function into original function, we get the below, note in my implementation of the formula, I set N top moves to be max of 5 to reduce computation time, if we take all legal moves then the idea of candidate moves is lost from original function, given usually there are few top candidates in a position and it makes calculation simpler.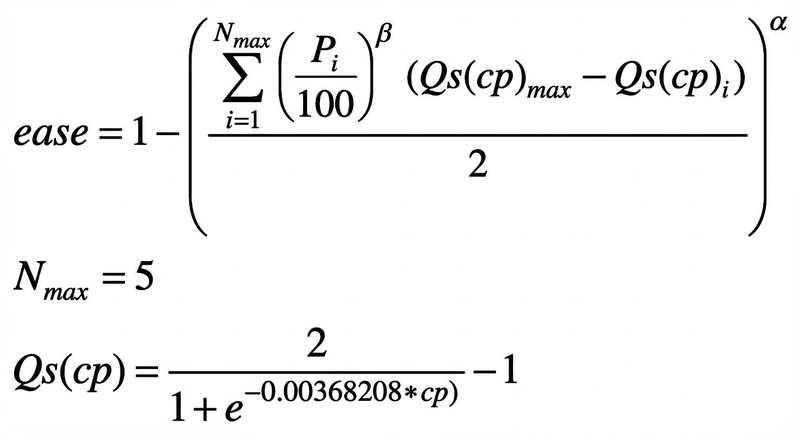

(We can swap original Q with Qs function, as now the plan is to take Stockfish's cp and convert it into Q, we can find Qs max out N Qs by using a simple max finding function, note Qs max is the max of all candidate moves of Qi)

Writing the code

I implemented this formula in code to calculate this ease metric from the values of Stockfish and Leela policy values. I defined a strategy calculator class that will act as a parent to any child of implementing the ease metric strategy. I was able to compute the extended ease metric formula for ChessDB also. Below is the code that computes the above function in TypeScript.

The Strategy class

export class EaseMetricStrategy {

    private debugLog: boolean;
    private calculatorName: string;

    constructor(log: boolean, name: string){
        this.debugLog = log;
        this.calculatorName = name;
    }

    protected calculateRawWinningChanceQ(cp: number) {
      const MULTIPLIER = -0.00368208; // https://github.com/lichess-org/lila/pull/11148
      return 2 / (1 + Math.exp(MULTIPLIER * cp)) - 1;
    };

    protected calculateSumOfMetrics (metrics: number[]) {
        return metrics.reduce((acc, val) => acc + val, 0);
    }

    protected calculateNodeEaseMetric(P: number, Qmax: number, Qi: number) {
        const PiCal = Math.pow(P, 1.5);
        const Qdiff = Math.max(0, Qmax - Qi);
        const component = (PiCal * Qdiff) / 2;
        const easeMetric = Math.pow(component, 1/3);

        return {
            easeMetric, component
        }
    }

    protected doLog(content: string){
       if(this.debugLog){
         console.log(`${this.calculatorName}: ${content}`);
       }
    }

}

The Stockfish integrated class

import { MaiaEvaluation } from "../nets/types";
import { EaseMetricStrategy } from "./easeMetricStrategy";
import { PositionEval } from "@/stockfish/engine/engine";

export class StockfishEaseMetricCalculator extends EaseMetricStrategy {

    constructor(log: boolean) {
        super(log, 'calculateEaseMetricFish');
    }

    public findMaxQ(engineEval: PositionEval): number {
        const maxQs = [];
        for (let i = 0; i < engineEval.lines.length; i++) {
            const cp = engineEval.lines[i].cp;
            maxQs.push(this.calculateRawWinningChanceQ(cp || 0));
        }

        return Math.max(...maxQs);
    }

    public calculateEaseMetric(
        netEvals: MaiaEvaluation,
        engineEval: PositionEval | null,
    ): number {
        if (!engineEval) {
            this.doLog('ChessDB candidate move for this move not found!');
            return 0;
        }

        const Qmax = this.findMaxQ(engineEval);
        console.info(
            `Qmax=${Qmax}, analyzing ${engineEval.lines.length} lines`,
        );

        const metrics: number[] = [];

        for (let i = 0; i < engineEval.lines.length; i++) { // here the length of lines is max of 5
            const move = engineEval.lines[i].pv[0];
            const policyValue = netEvals.policy[move];

            const P = policyValue > 1 ? policyValue / 100 : policyValue;
            const Qi = this.calculateRawWinningChanceQ(engineEval.lines[i].cp || 0);

            if (isNaN(Qi) || isNaN(P)) {
                this.doLog(
                    `Invalid values for move ${move}: P=${P}, Qi=${Qi}`,
                );
                continue;
            }

            const { easeMetric, component } = this.calculateNodeEaseMetric(
                P,
                Qmax,
                Qi,
            );

            if (isNaN(easeMetric)) {
                this.doLog(
                    `NaN metric for move ${move}: component=${component}`,
                );
                continue;
            }
            this.doLog(
                `move=${move}, P=${P.toFixed(4)}, Qi=${Qi.toFixed(4)}, metric=${easeMetric.toFixed(4)}`,
            );
            metrics.push(easeMetric);
        }

        if (metrics.length === 0) {
            this.doLog("calculateEaseMetric: No valid metrics calculated");
            return 0;
        }

        const metricMinusSum = this.calculateSumOfMetrics(metrics);

        const result = 1 - metricMinusSum;

        return result;
    }
}

The chessDB integration class

import { CandidateMove } from "../agine/helper";
import { EaseMetricStrategy } from "./easeMetricStrategy";
import { MaiaEvaluation } from "../nets/types";

export class ChessDBEaseMetricCalculator extends EaseMetricStrategy {
  

  constructor(log: boolean) {
    super(log, 'calculateEaseMetricDB');
  }

  public findMaxQ(chessDbEval: CandidateMove[]): number {
    const maxQs = [];
    for (let i = 0; i < chessDbEval.length; i++) {
      const cp = chessDbEval[i].rawEval || 0;
      maxQs.push(this.calculateRawWinningChanceQ(cp));
    }

    return Math.max(...maxQs);
  }

  public calculateEaseMetric(
    netEvals: MaiaEvaluation,
    chessDbEval: CandidateMove[] | null,
  ): number {
    try {
      if (!chessDbEval || chessDbEval.length === 0) {
        this.doLog('No engine evaluation provided');
        return 0;
      }

      const limitedMoves = chessDbEval.slice(0, 4); // we try to limit N max to 4 or 5 still reasonable to compute

      const Qmax = this.findMaxQ(limitedMoves);
      this.doLog(
        `calculateEaseMetricDB: Qmax=${Qmax}, analyzing ${chessDbEval.length} moves`,
      );

      const metrics: number[] = [];

      for (let i = 0; i < limitedMoves.length; i++) {
        const currNode = limitedMoves[i];
        const move = currNode.uci
        const policyValue = netEvals.policy[move];

        const P = policyValue > 1 ? policyValue / 100 : policyValue;
        const Qi = this.calculateRawWinningChanceQ(currNode.rawEval || 0);

        if (isNaN(Qi) || isNaN(P)) {
         
            this.doLog(
              `calculateEaseMetricDB: Invalid values for move ${move}: P=${P}, Qi=${Qi}`,
            );
          
          continue;
        }

        const { easeMetric, component } = this.calculateNodeEaseMetric(
          P,
          Qmax,
          Qi,
        );

        if (isNaN(easeMetric)) {
         
            this.doLog(
              `calculateEaseMetricDB: NaN metric for move ${move}: component=${component}`,
            );
          
          continue;
        }
        
          this.doLog(
            `calculateEaseMetricDB: move=${move}, P=${P.toFixed(4)}, Qi=${Qi.toFixed(4)}, metric=${easeMetric.toFixed(4)}`,
          );
        
        metrics.push(easeMetric);
      }

      if (metrics.length === 0) {
          this.doLog("calculateEaseMetricDB: No valid metrics calculated");
        
        return 0;
      }

      const metricMinusSum = this.calculateSumOfMetrics(metrics);

      const result = 1 - metricMinusSum;

      return result;
    } catch (err: unknown) {
      return 0;
    }
  }
}

see entire code on ChessAgine GitHub. Note this code is open source, and under the GPL-3.0 License, in case if anyone wants to build on top of my code

Sample position

Here is a sample position

Hard Lichess Puzzle 2500+

Hard Lichess Puzzle

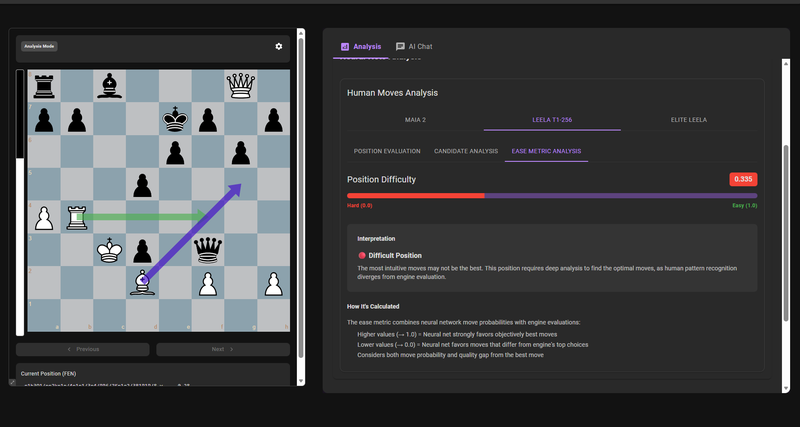
A value of 0.335 is given as ease, meaning a hard position

N Extended Ease Metric

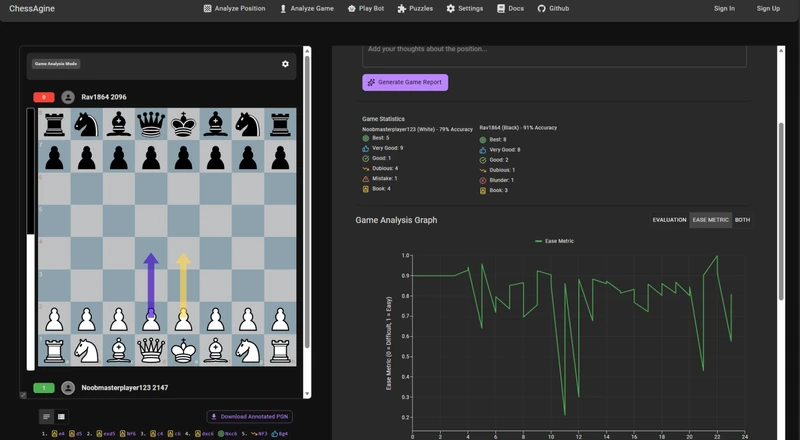
I took the calculations to the next level by computing this extended ease metric over N moves in a game. You can easily find where critical or hard positions occurred using the ease metric graph. Mathematically, this can be written as follows, lets consider N to be a 40-move game. We can write the logic to store the ease metric and then compute a line graph for ease metrics.

Below, we can see the actual line graph in the game review eval graph tab. As you can see, moves 12 and 21 had really hard positions in the entire game.

Conclusion

This concludes my analysis of my extended ease metric function based on the original ease metric. By integrating Stockfish and ChessDB, I was able to identify actual candidate moves, and by applying the converter function to Qi, I could also incorporate how the engine's winning chances compare to Leela T1-256's policy output, and setting Nmax for candidate moves to 5 helped with computation steps, making the calculations faster to show the metric to the end user. By writing the N Extended Ease Metric function, I was also able to code an algorithm that helps chess players to find critical/hard positions that have occurred
during a chess game.

I want to note that this function isn't perfect. I integrated Stockfish and ChessDB so I could view the ease metric directly in my chess GUI. Given that I'm using a small Leela T1-256 browser net, the results might not be entirely accurate, but after testing with several positions, it's still better than having nothing at all. I shared my work with @matstc in Lichess DMs, and they were quite happy with the outcome. Looking ahead, I want to write an inverse function that takes an ease metric and computes a Lichess puzzle rating. This could potentially give us a way to generate puzzles or enable further analysis, but that's a project for the future!

Thanks for reading,

Noob

Credits:

@matstc - Ease Metric Author
@SnowballSH - Converter function Author
Lichess Lila PR Converter function PR